前言
"color: #ff0000">1. BF算法
"application/x-tex">Bruce-ForceBruce"application/x-tex">S=ABACABABS=ABACABAB,模式串
def BF(substrS, substrT):
if len(substrT) > len(substrS):
return -1
j = 0
t = 0
while j < len(substrS) and t < len(substrT):
if substrT[t] == substrS[j]:
j += 1
t += 1
else:
j = j - t + 1
t = 0
if t == len(substrT):
return j - t
else:
return -1
2. KMP算法
"normal">.
"normal">"
"false">(
"normal">′
"text-align: center"> "text-align: left">"text-align: center">
"text-align: left">"text-align: center">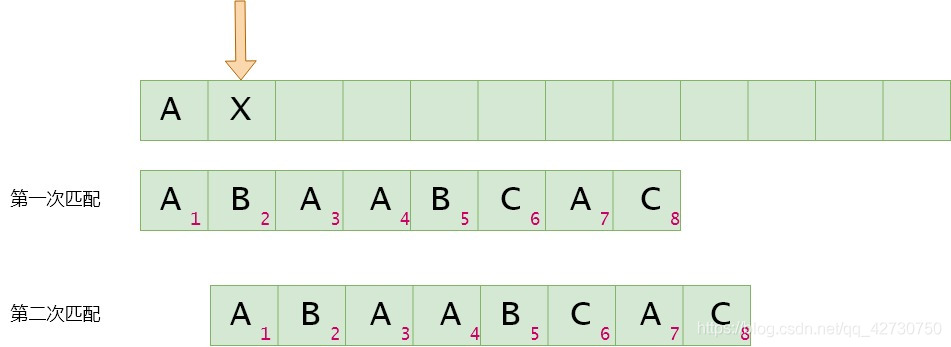 "text-align: left">"normal">"
"text-align: left">"normal">"
"normal">"
 "text-align: left">"normal">"
"text-align: left">"normal">"
"normal">"
"normal">"
"normal">"
 "text-align: left">如果模式串8号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为
"text-align: left">如果模式串8号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为
"text-align: left">
位编号
1
2
3
4
5
6
7
8
索引
0
1
2
3
4
5
6
7
模式串
A
B
A
A
B
C
A
C
next
-1
0
0
1
1
2
0
1
"text-align: center"> "text-align: left">"application/x-tex">T_j=T_tTj"false">[
"text-align: left">"application/x-tex">T_j=T_tTj"false">[
"normal">≠
"htmlcode">
def getNext(substrT):
next_list = [-1 for i in range(len(substrT))]
j = 0
t = -1
while j < len(substrT) - 1:
if t == -1 or substrT[j] == substrT[t]:
j += 1
t += 1
# Tj=Tt, 则可以到的next[j+1]=t+1
next_list[j] = t
else:
# Tj!=Tt, 模式串T索引为t的字符与当前位进行匹配
t = next_list[t]
return next_list
def KMP(substrS, substrT, next_list):
count = 0
j = 0
t = 0
while j < len(substrS) and t < len(substrT):
if substrS[j] == substrT[t] or t == -1:
# t == -1目的就是第一位匹配失败时
# 主串位置加1, 匹配串回到第一个位置(索引为0)
# 匹配成功, 主串和模式串指针都后移一位
j += 1
t += 1
else:
# 匹配失败, 模式串索引为t的字符与当前位进行比较
count += 1
t = next_list[t]
if t == len(substrT):
# 这里返回的是索引
return j - t, count+1
else:
return -1, count+1
3. KMP算法优化版
"application/x-tex">S=AAABAAAABS=AAABAAAAB,模式串

"text-align: left">"application/x-tex">SS的4号位为模式串
"false">[
def getNextval(substrT):
nextval_list = [-1 for i in range(len(substrT))]
j = 0
t = -1
while j < len(substrT) - 1:
if t == -1 or substrT[j] == substrT[t]:
j += 1
t += 1
if substrT[j] != substrT[t]:
# Tj=Tt, 但T(j+1)!=T(t+1), 这个就和next数组计算时是一样的
# 可以得到nextval[j+1]=t+1
nextval_list[j] = t
else:
# Tj=Tt, 且T(j+1)==T(t+1), 这个就是next数组需要更新的
# nextval[j+1]=上一次的nextval_list[t]
nextval_list[j] = nextval_list[t]
else:
# 匹配失败, 模式串索引为t的字符与当前位进行比较
t = nextval_list[t]
return nextval_list
"htmlcode">
if __name__ == '__main__':
S1 = 'ABACABAB'
T1 = 'ABAB'
S2 = 'AAABAAAAB'
T2 = 'AAAAB'
print('*' * 50)
print('主串S={0}与模式串T={1}进行匹配'.format(S1, T1))
print('{:*^25}'.format('KMP'))
next_list1 = getNext(T1)
print('next数组为: {}'.format(next_list1))
index1_1, count1_1 = KMP(S1, T1, next_list1)
print('匹配到的位置(索引): {}, 匹配次数: {}'.format(index1_1, count1_1))
print('{:*^25}'.format('KMP优化版'))
nextval_list1 = getNextval(T1)
print('nextval数组为: {}'.format(nextval_list1))
index1_2, count1_2 = KMP(S1, T1, nextval_list1)
print('匹配到的位置(索引): {}, 匹配次数: {}'.format(index1_2, count1_2))
print('')
print('*' * 50)
print('主串S={0}与模式串T={1}进行匹配'.format(S2, T2))
print('{:*^25}'.format('KMP'))
next_list2 = getNext(T2)
print('next数组为: {}'.format(next_list2))
index2_1, count2_1 = KMP(S2, T2, next_list2)
print('匹配到的位置(索引): {}, 匹配次数: {}'.format(index2_1, count2_1))
print('{:*^25}'.format('KMP优化版'))
nextval_list2 = getNextval(T2)
print('nextval数组为: {}'.format(nextval_list2))
index2_2, count2_2 = KMP(S2, T2, nextval_list2)
print('匹配到的位置(索引): {}, 匹配次数: {}'.format(index2_2, count2_2))
"application/x-tex">S=ABACABABS=ABACABAB与模式串
结束语
在写本篇博客之前也是反复看参考书、视频,边画图边去理解它,这篇博客也是反复修改了好几次,最终算是把KMP解决掉了,有关字符串知识的复习也算是基本结束,下面就是刷题了(虽然在LeetCode做过了几道题)。
Python,KMP
免责声明:本站文章均来自网站采集或用户投稿,网站不提供任何软件下载或自行开发的软件! 如有用户或公司发现本站内容信息存在侵权行为,请邮件告知! 858582#qq.com
P70系列延期,华为新旗舰将在下月发布
3月20日消息,近期博主@数码闲聊站 透露,原定三月份发布的华为新旗舰P70系列延期发布,预计4月份上市。
而博主@定焦数码 爆料,华为的P70系列在定位上已经超过了Mate60,成为了重要的旗舰系列之一。它肩负着重返影像领域顶尖的使命。那么这次P70会带来哪些令人惊艳的创新呢?
根据目前爆料的消息来看,华为P70系列将推出三个版本,其中P70和P70 Pro采用了三角形的摄像头模组设计,而P70 Art则采用了与上一代P60 Art相似的不规则形状设计。这样的外观是否好看见仁见智,但辨识度绝对拉满。
更新日志
- 小骆驼-《草原狼2(蓝光CD)》[原抓WAV+CUE]
- 群星《欢迎来到我身边 电影原声专辑》[320K/MP3][105.02MB]
- 群星《欢迎来到我身边 电影原声专辑》[FLAC/分轨][480.9MB]
- 雷婷《梦里蓝天HQⅡ》 2023头版限量编号低速原抓[WAV+CUE][463M]
- 群星《2024好听新歌42》AI调整音效【WAV分轨】
- 王思雨-《思念陪着鸿雁飞》WAV
- 王思雨《喜马拉雅HQ》头版限量编号[WAV+CUE]
- 李健《无时无刻》[WAV+CUE][590M]
- 陈奕迅《酝酿》[WAV分轨][502M]
- 卓依婷《化蝶》2CD[WAV+CUE][1.1G]
- 群星《吉他王(黑胶CD)》[WAV+CUE]
- 齐秦《穿乐(穿越)》[WAV+CUE]
- 发烧珍品《数位CD音响测试-动向效果(九)》【WAV+CUE】
- 邝美云《邝美云精装歌集》[DSF][1.6G]
- 吕方《爱一回伤一回》[WAV+CUE][454M]







